Desvio Padrão: A Chave para Entender a Variabilidade dos Seus Dados em IA

```html

Decifrando a Dispersão dos Dados: O que é Desvio Padrão?

No universo da análise de dados e Inteligência Artificial, a média é frequentemente a estrela do show. Ela nos oferece um ponto de referência, um centro de gravidade. Contudo, confiar apenas na média é como descrever uma cidade vibrante falando apenas de sua praça central — você perde toda a riqueza e diversidade dos bairros ao redor. É exatamente aqui que o Desvio Padrão assume o papel de protagonista.

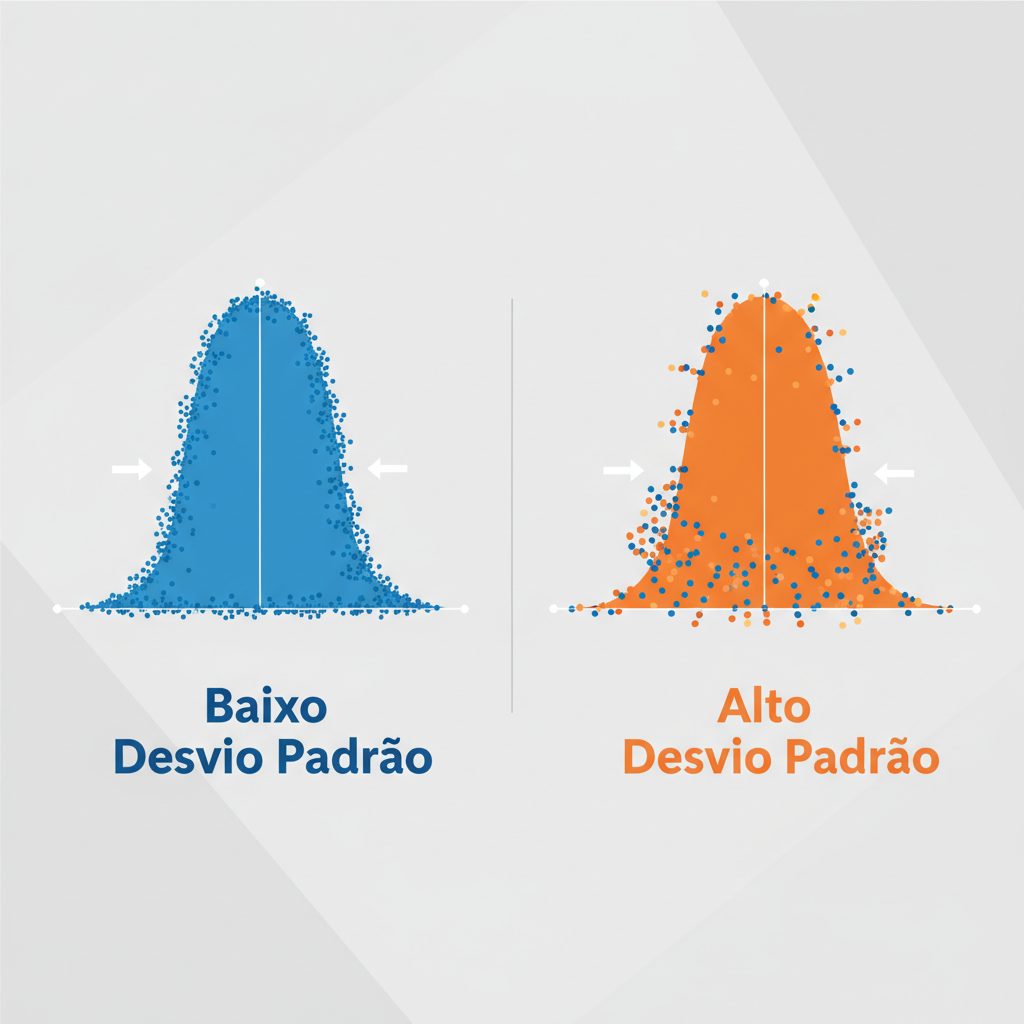
De forma simples, o desvio padrão é uma medida que quantifica o quão "espalhados" ou "dispersos" os valores de um conjunto de dados estão em relação à sua média. Um desvio padrão baixo indica que os dados estão firmemente agrupados, formando um conjunto coeso e previsível. Em contraste, um desvio padrão alto revela que os dados estão amplamente distribuídos, sinalizando uma grande variabilidade. Tecnicamente, ele é a raiz quadrada da variância, outra medida fundamental de dispersão.

A média nos diz onde fica o centro, mas o desvio padrão revela a personalidade dos dados ao redor dele.

Por que o Desvio Padrão é Crucial em Projetos de IA?

No campo da Inteligência Artificial e Machine Learning, entender a variabilidade dos dados não é um luxo, é uma necessidade. O desvio padrão é uma ferramenta indispensável no arsenal de qualquer cientista de dados para:

• Caçar Anomalias (Outliers): Pontos de dados que se afastam múltiplos desvios padrão da média são, frequentemente, anomalias ou *outliers*. Detectá-los é vital em sistemas de detecção de fraude, monitoramento de saúde de servidores ou controle de qualidade industrial.
• Normalizar e Padronizar Features: Muitos algoritmos, como SVMs e Redes Neurais, são sensíveis à escala das variáveis de entrada. A padronização (ou Z-score), que utiliza a média e o desvio padrão para reescalar os dados, garante que nenhuma feature domine o processo de aprendizado apenas por ter uma magnitude maior.
• Avaliar Risco e Volatilidade: No mercado financeiro, o desvio padrão do retorno de um ativo é a medida clássica de sua volatilidade e, por consequência, de seu risco. Um desvio padrão alto implica maior incerteza. Este conceito se estende a qualquer previsão, como estimar a demanda de um produto.
• Medir a Estabilidade de Modelos: Ao avaliar modelos com validação cruzada, analisamos não apenas a média do desempenho, mas também seu desvio padrão. Um desvio padrão baixo entre os *folds* (as divisões do dataset) sugere que o desempenho do modelo é estável e confiável em diferentes subconjuntos de dados.

Analogia Prática: A Confiabilidade de um Modelo Preditivo

Imagine que você treinou dois modelos de IA para prever o preço de ações. Nos testes, ambos apresentam uma média de erro de R$ 0,00 (ou seja, em média, eles acertam o alvo). Contudo, a análise mais profunda revela que:

• O Modelo A tem um desvio padrão de erro de R$ 2.
• O Modelo B tem um desvio padrão de erro de R$ 20.

Qual você escolheria? Embora as médias sejam idênticas, o Modelo A é imensamente mais confiável. Seus erros, quando ocorrem, são pequenos e consistentes. O Modelo B, por outro lado, é uma roleta-russa: pode acertar em cheio ou errar por uma margem gigantesca. O desvio padrão expõe essa perigosa inconsistência de forma cristalina.

Mãos à Obra: Desvio Padrão com Python e NumPy

A beleza da ciência de dados moderna é que não precisamos realizar cálculos complexos manualmente. Bibliotecas como a NumPy em Python tornam o processo trivial. Vamos analisar o desempenho de duas turmas de alunos para ver o desvio padrão em ação.

Conceitualmente, o cálculo segue estes passos:

1. Calcular a média do conjunto de dados.
2. Para cada ponto de dado, subtrair a média e elevar o resultado ao quadrado.
3. Calcular a média desses valores ao quadrado (isso nos dá a variância).
4. Tirar a raiz quadrada da variância para encontrar o desvio padrão.

Agora, veja como isso é simples com código:

import numpy as np

# Notas de duas turmas distintas
turma_a = [85, 88, 90, 84, 86, 87]
turma_b = [60, 75, 95, 100, 55, 80]

# Calculando a média e o desvio padrão para cada turma
media_a = np.mean(turma_a)
desvio_padrao_a = np.std(turma_a)

media_b = np.mean(turma_b)
desvio_padrao_b = np.std(turma_b)

print(f"Turma A -> Média: {media_a:.2f} | Desvio Padrão: {desvio_padrao_a:.2f}")
print(f"Turma B -> Média: {media_b:.2f} | Desvio Padrão: {desvio_padrao_b:.2f}")

# Saída do código:
# Turma A -> Média: 86.67 | Desvio Padrão: 2.05
# Turma B -> Média: 77.50 | Desvio Padrão: 16.52

A análise dos resultados é reveladora. A Turma A possui um desvio padrão muito baixo (2.05), indicando um desempenho notavelmente homogêneo; quase todos os alunos tiveram notas próximas da excelente média de 86.67. Por outro lado, a Turma B exibe um desvio padrão altíssimo (16.52), mostrando uma enorme disparidade. Há alunos com notas excelentes e outros com desempenho muito baixo. Para um gestor educacional, os dados da Turma B exigiriam uma investigação aprofundada para entender essa variabilidade e apoiar os alunos com dificuldades.

Conclusão: Mais que um Número, uma Lupa para Seus Dados

Dominar o conceito de desvio padrão é um passo transformador para quem deseja ir além da superfície na análise de dados. Ele oferece uma camada de profundidade que a média, sozinha, jamais consegue capturar, permitindo-nos avaliar consistência, identificar anomalias e, finalmente, construir modelos de IA mais robustos e confiáveis. Da próxima vez que se deparar com um conjunto de dados, não se contente com a média. Pergunte: "E qual é o desvio padrão?". A resposta, muitas vezes, contém a história mais interessante.

```